INTERPLANETARY FLIGHT

INTERPLANETARY FLIGHT

---

• Heliocentric Transfer Orbit
• The Gauss Problem
• Determining Orbital Elements
• Hyperbolic Departure and Approach
• Gravitational Assist

---

An interplanetary spacecraft spends most of its flight time moving under the gravitational influence of a single body – the Sun. Only for brief periods, compared with the total mission duration, is its path shaped by the gravitational field of the departure or arrival planet. The perturbations caused by the other planets while the spacecraft is pursuing its heliocentric course are negligible.

The computation of a precision orbit is a trial-and-error procedure involving numerical integration of the complete equations of motion where all perturbation effects are considered. For preliminary mission analysis and feasibility studies it is sufficient to have an approximate analytical method for determining the total V required to accomplish an interplanetary mission. The best method available for such analysis is called the patched-conic approximation.

The patched-conic method permits us to ignore the gravitational influence of the Sun until the spacecraft is a great distance from the Earth (perhaps a million kilometers). At this point its velocity relative to Earth is very nearly the hyperbolic excess velocity. If we now switch to a heliocentric frame of reference, we can determine both the velocity of the spacecraft relative to the Sun and the subsequent heliocentric orbit. The same procedure is followed in reverse upon arrival at the target planet's sphere of influence.

The first step in designing a successful interplanetary trajectory is to select the heliocentric transfer orbit that takes the spacecraft from the sphere of influence of the departure planet to the sphere of influence of the arrival planet.

If you have not already done so, before continuing it is recommended that you first study the Orbital Mechanics section of this web site. It is also recommended, if you are not already familiar with the subject, that you review our section on Vector Mathematics.

Heliocentric-Ecliptic Coordinate System

Our first requirement for describing an orbit is a suitable inertial reference frame. In the case of orbits around the Sun, such as planets, asteroids, comets and some deep-space probes describe, the heliocentric-ecliptic coordinate system is convenient. As the name implies, the heliocentric-ecliptic system has its origin at the center of the Sun. The X-Y or fundamental plane coincides with the ecliptic, which is the plane of Earth's revolution around the Sun. The line-of-intersection of the ecliptic plane and Earth's equatorial plane defines the direction of the X-axis. On the first day of spring a line joining the center of Earth and the center of the Sun points in the direction of the positive X-axis. This is called the vernal equinox direction. The Y-axis forms a right-handed set of coordinate axes with the X-axis. The Z-axis is perpendicular to the fundamental plane and is positive in the north direction.

It is known that Earth wobbles slightly and its axis of rotation shifts in direction slowly over the centuries. This effect is known as precession and causes the line-of-intersection of Earth's equator and the ecliptic to shift slowly. As a result the heliocentric-ecliptic system is not really an inertial reference frame. Where extreme precision is required, it is necessary to specify that the XYZ coordinates of an object are based on the vernal equinox direction of a particular year or epoch.

Heliocentric Transfer Orbit

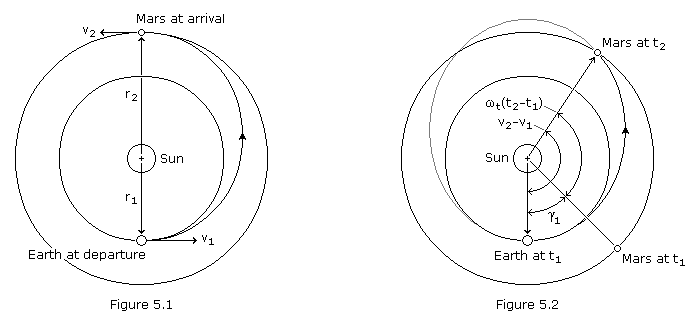
For transfers to most of the planets, we may initially consider that the planetary orbits are both circular and coplanar. In the Orbital Mechanics section of this site we discussed the problem of transferring between coplanar orbits and found that the most economical method, from the standpoint of V required, was the Hohmann transfer. A Hohmann transfer between Earth and Mars is pictured in Figure 5.1 below.

While it is generally desirable that the transfer orbit be tangential to Earth's orbit at departure, it may be preferable to intercept Mars' orbit prior to apogee, especially if the spacecraft is to return to Earth. The Hohmann transfer, if continued past the destination planet, would not provide a suitable return trajectory. For a one-way trip this is irrelevant; however, for a probe that is to be recovered or for a manned mission, this consideration is important. The outbound trip to Mars on the Hohmann trajectory consumes between 8 and 9 months. If the spacecraft continued its flight it would return to the original point of departure only to find Earth nearly on the opposite side of its orbit. Therefore, either the spacecraft must loiter in the vicinity of Mars for nearly 6 months or the original trajectory must be modified so that the spacecraft will encounter Earth at the point where it recrosses Earth's orbit.

If the spacecraft is to encounter the target planet at the time it crosses the planet's orbit then obviously Earth and the target planet must have the correct angular relationship at departure. The angle between the radius vectors to the departure and arrival planets is called 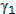, the phase angle at departure, and is pictured in Figure 5.2 for a Mars trajectory. The total sweep angle from departure to arrival is just the difference in the true anomaly at the two points, ₂–₁.

From Figure 5.2 we can see that the transfer is the one-tangent burn type, which we examined previously. Selecting a transfer orbit allows the determination of the change in true anomaly and the time-of-flight using equations (4.67) and (4.71).

Click here for example problem #5.1

The target planet will move through an angle of 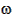_t(t₂–t₁) while the spacecraft is in flight, where 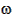_t is the angular velocity of the target planet. Thus, the correct phase angle at departure is,

Click here for example problem #5.2

The requirement that the phase angle at departure be correct severely limits the times when a launch may take place. The heliocentric longitudes of the planets are tabulated in The Astronomical Almanac, and these may be used to determine when the phase angle will be correct. Alternatively, the page Planet Positions provides the data and demonstrates the methods necessary to estimate planet positions without needing to refer to other sources.

Mars Transfer Trajectories

The methods described above provide only a very rough estimate of the phase angle, particularly in the case of Mars. The orbit of Mars is significantly eccentric, meaning its angular velocity changes considerably depending on whether it is near perihelion or aphelion at the time of transfer. For a better estimate we can no longer consider the orbit to be circular.

As can be seen from Figure 5.2, the proper alignment for a transfer to Mars occurs in the months just prior to an opposition. The location of Mars within its orbit at the time of opposition depends on the time of year the opposition occurs. Perihelion oppositions occur in the August-September time period, and aphelion oppositions occur in the February-March time period. We can, therefore, link the phase angle required to the time of year that we initiate the transfer.

Table 1 Date 2020 Phase Angle Actual (A) Figure 5.3 (B) A–B 5/1 57.0 34.0 23.0 6/1 45.7 29.0 16.7 7/1 35.6 28.0 7.6 8/1 25.6 32.0 -6.4 9/1 15.5 39.0 -23.5

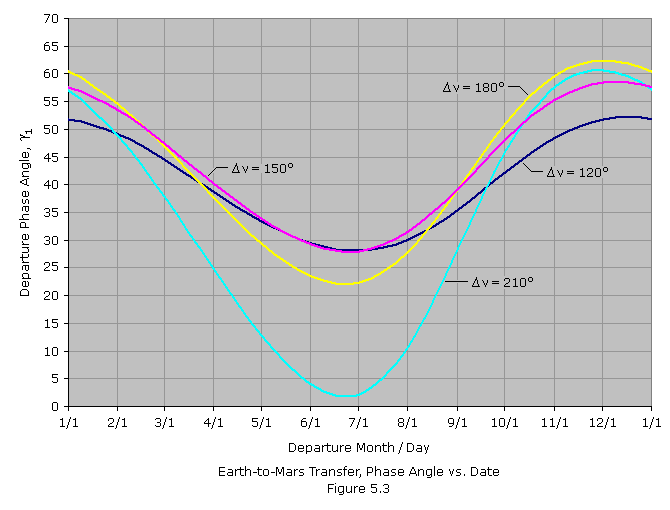
Figure 5.3 above is a chart showing departure phase angle versus departure calendar date. Four curves are shown, each representing a different transfer orbit. The trajectories are tangent to Earth's orbit at departure and differ in the number of degrees the spacecraft travels around the Sun before intercepting Mars, i.e. the change in true anomaly, . If the interplanetary trajectory carries the spacecraft less than 180 degrees around the Sun, it's called a Type-I trajectory. If the trajectory carries it 180 degrees or more around the Sun, it's called a Type-II. A Type-I trajectory is pictured in Figure 5.2. In a Type-II trajectory, the intercept point is at the second Mars orbit crossing.

Figure 5.3 gives the required phase angle for transfers departing on the dates listed across the bottom of the chart. To use Figure 5.3 it is necessary to find the date when the actual phase angle equals the required angle obtained from the chart. For example, let's say we are planning a mission to launch around the October-13 opposition of the year 2020. It's decided we'll use a Type-I trajectory in which the spacecraft's true anomaly change is 150 degrees (magenta curve). In Table 1 we list the actual Mars-Earth phase angle for the months leading up to the October opposition, along with the phase angle read from Figure 5.3. We see that there is a date in July when the two numbers are equal. We can interpolate that the departure date will be sometime in the third week of July and the departure phase angle will be approximately 30 degrees.

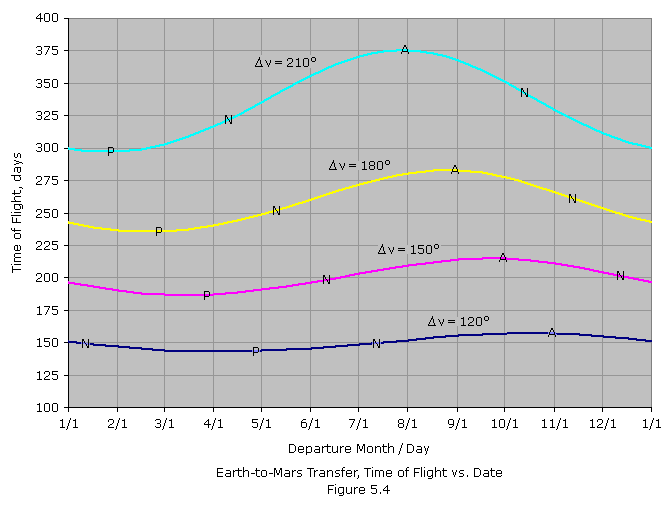
Just as phase angle is dependent on Mars' location within its orbit, so is the time of flight. After estimating the departure date from Figure 5.3, we can use Figure 5.4 below to estimate the flight duration. For instance, for the July departure window determined above, the time of flight for a trajectory with a true anomaly change of 150^o is found to be about 207 days. The letters superimposed on each curve indicate the departure dates that will result in the spacecraft intercepting Mars at perihelion (P), aphelion (A) or one of the two nodes (N).

Referring again Figure 5.2, we see that the flight path angle of the transfer orbit is positive at the first Mars orbit crossing and negative at the second Mars orbit crossing. Therefore, it may be preferable to use a Type-I trajectory when interception occurs with Mars in the part of its orbit past perihelion and approaching aphelion, when the planet's flight path angle is likewise positive. Conversely, a Type-II trajectory may be preferable when interception occurs with Mars in the part of its orbit past aphelion and approaching perihelion. Having Mars and spacecraft flight path angles both positive or both negative reduces the angle between the velocity vectors, and thus the relative velocity. This can be critical when V is the limiting factor. Of course a Type-I trajectory is always preferable when minimizing flight time is most critical.

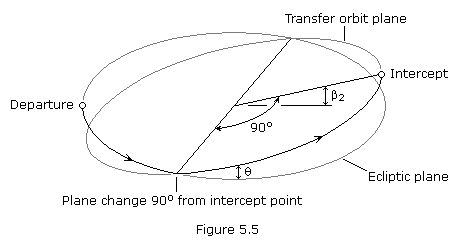
Non-coplanar Trajectories

Up to now we have assumed that the planetary orbits all lie in the plane of the ecliptic. However, we know that all planets other than Earth have orbits inclined to the ecliptic. A good procedure to use when the target planet lies above or below the ecliptic at intercept is to launch the spacecraft into a transfer orbit that lies in the ecliptic plane and then make a simple plane change during mid-course when the true anomaly change remaining to intercept is 90-degrees. This minimizes the magnitude of the plane change required and is illustrated in Figure 5.4 below. Since the plane change is made 90^o short of intercept, the required inclination is just equal to the ecliptic latitude, 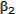, of the target planet at the time of intercept, t₂. The V required to produce a plane change was examined previously, and is calculated using equation (4.73).

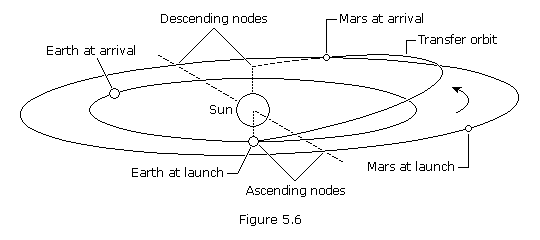
Alternatively, the injection maneuver that places the spacecraft on its interplanetary trajectory can include a plane change to correctly orient the plane of the transfer orbit to intercept the target planet. Such an orbit between Earth and Mars is pictured in Figure 5.6 below. Since Earth lies in the ecliptic plane, the departure point defines one of the transfer orbit's two nodes, with the other node 180 degrees away on the opposite side of the Sun. Unless the target planet happens to also be passing through one of its nodes at the time of interception, a near 180-degree transfer is not possible without a prohibitively high inclination. Intercepting the target with a true anomaly change several degrees less than 180^o (as pictured) or several degrees more than 180^o can be achieved with a manageably low inclination.

The Gauss Problem

On New Year's Day 1801, Giuseppe Piazzi of Italy observed for the first time an object that turned out to be the minor planet Ceres. He was only able to observe the asteroid for about one month before it was lost in the glare of the Sun. The challenge of rediscovering Ceres when it reappeared from behind the Sun seduced the intellect of young German mathematician Carl Friedrich Gauss. Exactly one year later, on New Year's Day 1802, Ceres was rediscovered precisely where the ingenious and detailed calculations of Gauss had predicted she must be found.

The method that Gauss used is just as pertinent today as it was in 1802, but for a different reason. The data that Gauss used to determine the orbit of Ceres consisted of the right ascension and declination at three observation times. His method is much simplified if the original data consists to two position vectors and the time-of-flight between them. The technique of determining an orbit from two position vectors and time is of considerable interest to modern astrodynamics since it has direct application in the solution of intercept and rendezvous.

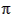We may define the Gauss problem as follows: Given position vectors r₁ and r₂, the time of flight from r₁ to r₂, which we will call t, and the direction of motion, find velocity vectors v₁ and v₂. By "direction of motion" we mean whether the satellite is to go from r₁ to r₂ the "short way", through an angular change () of less than radians, or the "long way", through an angular change greater than 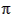radians. Obviously, there are an infinite number of orbits passing through r₁ and r₂, but only two that have the specified time-of-flight – one for each possible direction of motion.

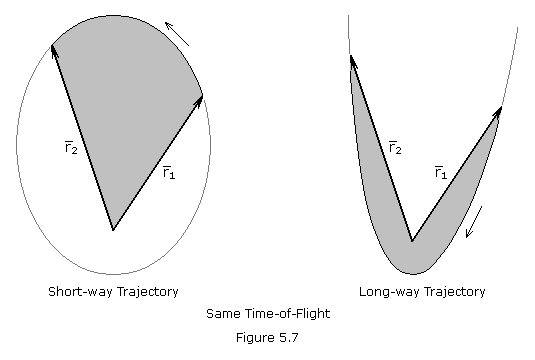
One thing is immediately obvious from Figure 5.7; the two vectors r₁ and r₂ uniquely define the plane of the transfer orbit. If the vectors r₁ and r₂ are collinear and in opposite directions (=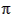), the plane of the transfer orbit is not determined and a unique solution for v₁ and v₂ is not possible. If the two position vectors are collinear and in the same direction (=0 or 2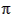), the orbit is a degenerate conic, but a unique solution is possible of v₁ and v₂.

The relationship between the four vectors r₁, r₂, v₁ and v₂ is contained in the f and g expressions given below. It is not surprising, therefore, that nearly every known method for solving the Gauss problem may be derived from the f and g relations.

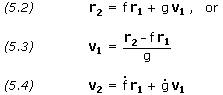
where,

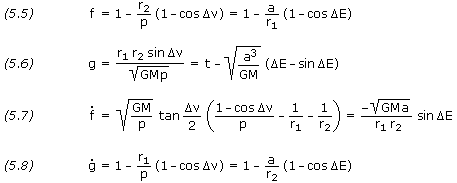
As previously defined, is true anomaly, E is eccentric anomaly, a is semi-major axis, and GM is the standard gravitational parameter, while p is a geometrical constant of the conic section called the parameter or semi-latus rectum.

Consider equations (5.5), (5.6) and (5.7). There are seven variables — r₁, r₂, , t, p, a and E — but the first four are known, so what we have is three equations in three unknowns. The only trouble is that the equations are transcendental in nature, so a trial-and-error solution is necessary. We may outline the general method of solution as follows:

• Guess a trial value for one of the three unknowns, p, a or E directly or indirectly by guessing some other parameter of the transfer orbit that in turn establishes p, a or E.
• Use equations (5.5) and (5.7) to compute the remaining two unknowns.
• Test the result by solving equation (5.6) for t and check it against the given value of time-of-flight.
• If the computed value of t does not agree with the given value, adjust the trial value of the iteration variable and repeat the procedure until it does agree.

The last step is perhaps the most important of all, since the method used to adjust the trial value of the iteration variable is what determines how quickly the procedure converges to a solution. There are several methods for solving the Gauss problem, however the only one we will present here is the p-iteration technique. The method consists of guessing a trial value of p from which we can compute a and E.

The first step in the solution is to find an expression for a as a function of p and the given information. We will find it convenient to define three constants that may be determined from the given information:

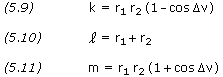
where r₁ = |r₁| and r₂ = |r₂|.

Once p is specified, a unique value of a is determined from

Once we have selected a trial value of p and computed a from equation (5.12), we are ready to solve for t and check it against the given time-of-flight. First, however, we need to determine E, or F in case a is negative (i.e. the orbit is hyperbolic).

From the trail value of p and the known information, we can compute f, g and 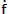from equations (5.5), (5.6) and (5.7). If a is positive, we can determine E from equations (5.5) and (5.7), rearranged as follows:

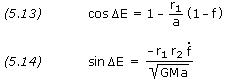
If a is negative, the corresponding f and g expressions involving F yield the following. Since we always assume F is positive, there is no ambiguity in determining F from this one equation.

The time-of-flight may now be determined from equation (5.16) or the corresponding equation involving F:

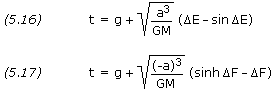
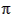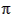The limiting values of p correspond to two parabolic orbits passing through r₁ and r₂. The values of p that specify the parabolic orbits we'll call p_i and p_ii. For less than radians, p must lie between p_i and infinity. For greater than radians, p must lie between 0 and p_ii. Since it is important that the first trial value, as well as all subsequent guesses for p, lie within the prescribed limits, we should first compute p_i or p_ii.

The method used to adjust the trial value of p to give the desired time-of-flight is crucial in determining how rapidly p converges to a solution. Several simple methods may be used successfully, such as the bisection or linear interpolation techniques.

In the bisection method we must find two trial values of p, one that gives too small a value for t and one that gives too large a value. The solution is then bracketed and, by choosing our next trial value half way between the first two, we can keep it bracketed while reducing the interval of uncertainty to some arbitrarily small value.

In the linear interpolation method we choose two trial values of p, which we will call p_n-1 and p_n. If t_n-1 and t_n are the times-of-flight corresponding to these trial values of p, then we select a new value from,

This scheme can be repeated, always retaining the latest two trial values of p and their corresponding times-of-flight for use in computing a still better trial value from equation (5.20). It is not necessary that the initial two trial values bracket the answer.

We can summarize the steps involved in solving the Gauss problem via the p-iteration technique as follows:

• Evaluate the constants k, 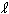and m from r₁, r₂ and using equations (5.9) through (5.11).
• Determine the limits on the possible values of p by evaluating p_i and p_ii from equations (5.18) and (5.19).
• Pick a trial value of p within the appropriate limits.
• Using the trial value of p, solve for a from equation (5.12). The type conic orbit will be known from the value of a.
• Solve for f, g and 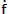from equations (5.5), (5.6) and (5.7).
• Solve for E or F, as appropriate, using equations (5.13) and (5.14) or equation (5.15).
• Solve for t from equation (5.16) or (5.17) and compare it with the desired time-of-flight.
• Adjust the trial value of p using one of the iteration methods discussed above until the desired time-of-flight is obtained.
• Evaluate 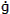from equation (5.8) and then solve for v₁ and v₂ using equations (5.3) and (5.4).

The p-iteration method converges in all cases except when r₁ and r₂ are collinear. Its main disadvantage is that separate equations are used for the ellipse and hyperbola.

Click here for example problem #5.3 

Click here for example problem #5.4

Selecting a Transfer Orbit

Each time the Gauss problem is solved, the result gives just one of an infinite number of possible transfer orbits. It was previously stated that it generally desirable that the transfer orbit be tangential to Earth's orbit at departure. This is true only in that it minimizes the V required to inject the spacecraft into its transfer orbit; however, it likely results in a less than optimum condition at target intercept. A one-tangent burn produces a trajectory that crosses the orbit of the target planet with a relatively large flight path angle, resulting in a large relative velocity between the spacecraft and planet. This relative velocity can be significantly reduced by selecting a transfer orbit that reduces the angle between the velocity vectors of the spacecraft and target at the moment of intercept. Improving the intercept condition (1) increases the duration of a close flyby encounter, (2) reduces the V required for orbit insertion, or (3) lowers the spacecraft's velocity at atmospheric entry.

Tables 2 and 3 below provide sample data for a hypothetical mission to Mars in the year 2020. Table 2 gives the V required for Trans-Mars Injection (TMI) for a variety of different departure dates and times of flight. TMI is the maneuver that places the spacecraft into a trajectory that will intercept Mars at the desired place and time. In this sample, it is assumed that TMI is performed from an Earth parking orbit with an altitude of 200 km. Table 3 gives the V required for Mars-Orbit Insertion (MOI) for the same departure dates and times of flight found in Table 2. MOI, as it names implies, is the maneuver that slows the spacecraft to a velocity that places it into the desired orbit around Mars. In this sample, it is assumed that MOI is performed at periapsis of a insertion orbit with a periapsis altitude of 1,000 km and an apoapsis altitude of 33,000 km. Placing a spacecraft into a high eccentricity orbit such as this is common, as it provides for a MOI burn with a relatively low V.

Table 2
Trans-Mars Injection DV (m/s), launch altitude = 200 km
Departure Date, 2020	Time of Flight (days)
	180	185	190	195	200	205	210	215	220	225	230
7/7	3876	3862	3854	3851	3853	3863	3881	3912	3962	4043	4180
7/12	3841	3830	3824	3823	3826	3835	3851	3877	3917	3978	4074
7/19	3819	3812	3808	3808	3811	3819	3833	3853	3882	3925	3988
7/26	3834	3829	3826	3826	3829	3836	3846	3862	3883	3913	3956
8/2	3892	3887	3885	3884	3886	3890	3897	3908	3923	3943	3972
8/9	3999	3994	3990	3987	3987	3987	3991	3996	4005	4017	4034
8/16	4162	4154	4147	4141	4137	4133	4131	4131	4133	4138	4146
8/23	4386	4373	4362	4351	4341	4332	4325	4318	4313	4310	4309

Table 3
Mars Orbit Insertion DV (m/s), insertion orbit = 1000 × 33000 km
Departure Date, 2020	Time of Flight (days)
	180	185	190	195	200	205	210	215	220	225	230
7/7	1371	1258	1163	1086	1025	982	959	957	984	1052	1187
7/12	1290	1188	1102	1033	979	940	918	915	933	982	1074
7/19	1186	1097	1024	965	920	888	870	866	879	911	970
7/26	1093	1019	957	909	872	847	833	830	840	864	905
8/2	1016	954	904	865	837	818	808	808	817	836	867
8/9	957	907	868	838	817	804	799	801	811	828	853
8/16	920	881	852	830	816	809	808	813	823	839	862
8/23	910	881	860	846	838	836	839	846	857	873	893

As can be seen from Tables 2 and 3, in most instances, TMI V and MOI V are inversely proportional. That is, trying to optimize one increases the other, and vice versa. Selecting the "best" transfer orbit therefore comes down to making a compromise. The size of the launch window is also often limited by the V budget. For example, suppose our launch vehicle can deliver no more than 3,900 m/s for TMI, and our spacecraft's MOI budget is 900 m/s. Our potential launch opportunities are limited to those in which both of these conditions are met, which we see represented by the launch dates and flight durations highlighted above.

Determining Orbital Elements

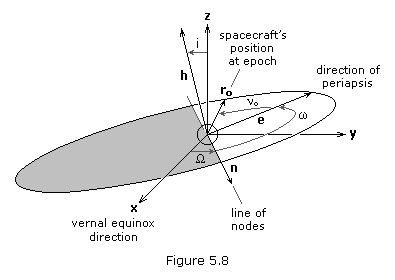
Solving the Gauss problem gives us the position and velocity vectors, r and v, of a spacecraft in a heliocentric-ecliptic orbit. From these vectors we can determine the six orbital elements that describe the motion of the satellite. The first step is to form the three vectors, h, n and e, illustrated in Figure 5.08.

The specific angular momentum, h, of a satellite is obtained from

It is important to note that h is a vector perpendicular to the plane of the orbit.

The node vector, n, is defined as

From the definition of a vector cross product, n must be perpendicular to both z and h. To be perpendicular to z, n would have to lie in the ecliptic plane. To be perpendicular to h, n would have to lie in the orbital plane. Therefore, n must lie in both the ecliptic and orbital planes, or in their intersection, which is called the "line of nodes." Specifically, n is a vector pointing along the line of nodes in the direction of the ascending node. The magnitude of n is of no consequence to us; we are only interested in its direction.

The third vector, e, is obtained from

Vector e points from the center of the Sun (focus of the orbit) toward perihelion with a magnitude exactly equal to the eccentricity of the orbit.

Now that we have h, n and e we can preceed rather easily to obtain the orbital elements. The semi-major axis, a, and the eccentricity, e, follow directly from r, v, and e, while all the remaining orbital elements are simply the angles between two vectors whose components are now known. If we know how to find the angle between two vectors the problem is solved. In general, the cosine of the angle, 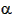, between two vectors a and b is found by dividing the dot product of the two vectors by the product of their magnitudes.

Of course, being able to evaluate the cosine of an angle does not mean that we know the angle. We still have to decide whether the angle is smaller or greater than 180 degrees. The answer to this quadrant resolution problem must come from other information in the problem as we shall see.

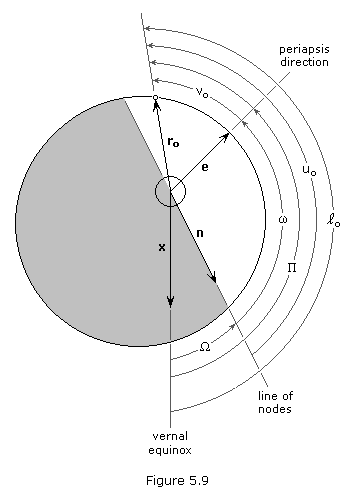
We can outline the method of finding the orbital elements as follows:

• Calculate a and e,

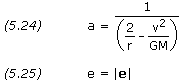
• Since i is the angle between z and h,

(Inclination is always less than 180^o)

• Since 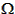is the angle between x and n,

(If n_y > 0 then is less than 180^o)

• Since 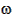is the angle between n and e,

(If e_z > 0 then is less than 180^o)

• Since _o is the angle between e and r,

(If r • v > 0 then _o is less than 180^o)

• Since u_o is the angle between n and r,

(If r_z > 0 then u_o is less than 180^o)

• Calculate and _o,

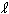( and _o are always less than 360^o)

The angle 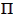, longitude of periapsis, is sometimes used in place of argument of periapsis. As a substitute for the time of periapsis passage, any of the following may be used to locate the spacecraft at a particular time, t_o, known as the "epoch": _o, true anomaly at epoch, u_o, argument of latitude at epoch, or 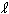_o, true longitude at epoch.

If there is no periapsis (circular orbit), then 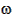is undefined, and 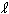_o = 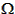+ u_o. If there is no ascending node (equatorial orbit), then both 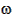and u_o are undefined, and 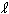_o = + _o. If the orbit is both circular and equatorial, _o is simply the true angle from x to r_o, both of which are always defined.

Click here for example problem #5.5

The procedure outlined above describes a spacecraft in a solar orbit, but the method works equally well for satellites in Earth orbit, or around another planet or moon, where the position and velocity vectors are known in the geocentric-equatorial reference plane. Note, however, that it is customary for the geocentric-equatorial coordinate system to use unit vectors i, j and k instead of x, y and z as used in the heliocentric-ecliptic system.

Hyperbolic Departure and Approach

Solving the Gauss problem gives us the heliocentric transfer orbit that takes the spacecraft from the sphere of influence of the departure planet to the sphere of influence of the arrival planet. To complete the patched-conic method, we will now examine the trajectories within the planets' spheres of influence. For this discussion we will assume the departure planet is Earth, though the methods described apply equally to other departure planets.

Escape from Earth's Sphere of Influence

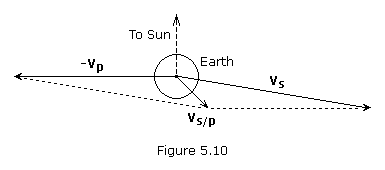
Once the heliocentric transfer orbit has been selected, we next determine the spacecraft's velocity relative to Earth. The relative velocity, which we will define as the vector v_s/p, is the difference between the spacecraft's heliocentric velocity, v_s, and the planet's orbital velocity, v_p (see Figure 5.10).

where the vector magnitude is,

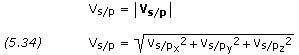
We can now proceed to establish the injection or launch conditions near the surface of Earth that will result in the required hyperbolic excess velocity. Since Earth's sphere of influence has a radius about one million kilometers, we assume that V_∞ ≈ V_s/p. Combining equations (4.78) and (4.88), we can solve for the injection velocity, V_o, as follows:

If launch occurs from an Earth parking orbit, the injection V is simply the injection velocity minus the orbital velocity,

The hyperbolic excess velocity is extremely sensitive to small errors in the injection velocity. For a Hohmann transfer to Mars, a one percent error in injection velocity results in a 15 percent error in hyperbolic excess velocity.

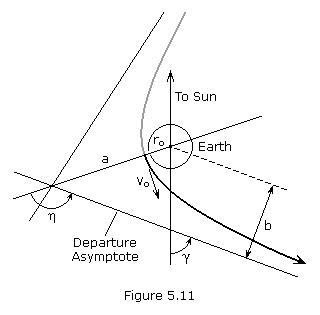
The departure asymptote should be parallel to the hyperbolic excess velocity, as shown in Figure 5.11. The zenith angle of the asymptote, 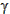, is obtained from the dot product r • v_s/p.

Click here for example problem #5.6

To determine the further parameters of the hyperbolic escape trajectory, please refer to the hyperbolic orbit as previously examined.

Arrival at the Target Planet

As before, the relative velocity vector and magnitude are calculated using equations (5.33) and (5.34).

If a dead center hit on the target planet is planned, then we solve the Gauss problem setting r₂ equal to the position vector of the planet at arrival. This ensures that the target planet will be at the intercept point at the same time the spacecraft is there. It also means that the relative velocity vector, upon arrival at the target planet's sphere of influence, will be directed toward the center of the planet, resulting in a straight line hyperbolic approach trajectory.

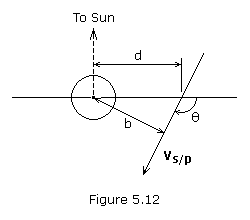
If it is desired to fly by the planet instead of impacting it, then the transfer trajectory must be modified so that the spacecraft crosses the target planet's orbit ahead of or behind the planet. If the spacecraft crosses the planet's orbit a distance d from the planet, then the velocity vector v_s/p, which represents the hyperbolic excess velocity on the approach hyperbola, is offset a distance b from the center of the target planet, as shown in Figure 5.12.

The sign of d is chosen depending on whether the spacecraft is to cross ahead of (positive) or behind (negative) the target planet. Assuming the target point lies within the same X-Y plane as the planet, the rectangular components of d are,

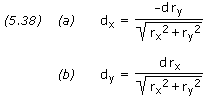
where r_x and r_y are scalar components of the planet's position vector.

The angle is calculated as follows:

From the following we obtain the impact parameter, b

Recalling that V_∞ ≈ V_s/p, we calculate the hyperbola's semi-major axis and eccentricity as follows:

Click here for example problem #5.7

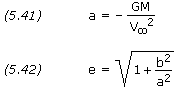
To calculate the remaining parameters of the hyperbolic approach trajectory, see the hyperbolic orbit.

For a close flyby, and understanding that the patched-conic method is only an approximate solution, it is generally adequate to ignore the miss distance, d, when solving the Gauss problem, assuming the position vector at arrival is equal to that of the planet. However, if the flyby distance is large, an improved Gauss solution is obtained by modifying the position vector to account for miss distance. If r_x, r_y and r_z are the scalar components of the planet's position vector, the components of the target point, r_x', r_y' and r_z', are as follows:

Gravitational Assist

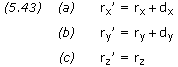
In planning certain types of trajectories of spacecraft within the solar system, engineers rely on a technique called gravitational assist (also gravity assist, slingshot, or swing-by). This technique underlies the feasibility of effecting a net change in both the speed and direction of motion of a spacecraft by passage through the gravitational field of a planet or a planetary satellite, typically in order to save propellant, time, and expense.

A gravitational assist around a planet changes a spacecraft's velocity relative to the Sun by entering and leaving the gravitational field of a planet. The spacecraft accelerates as it approaches the planet and decelerates while escaping its gravitational pull. Because the planet orbits the Sun, this motion affects the spacecraft during the maneuver. To accelerate, the spacecraft flies across the trailing side of the planet, taking a small amount of the planet's orbital energy (as pictured in Figure 5.13). To decelerate, the spacecraft flies across the leading side of the planet. The sum of the kinetic energies of both bodies remains constant. A gravitational assist can therefore be used to change the spaceship's trajectory and speed relative to the Sun.

The resulting increase, or decrease, in the kinetic energy of the spacecraft appears to contradict the casual expectation that in such an encounter the kinetic energy of the spacecraft after the encounter would be the same as that before the encounter. However, the energy gained by the spaceship is equal in magnitude to that lost by the planet, though the planet's enormous mass compared to the spacecraft makes the resulting change in its speed negligibly small. These effects on the planet are so slight that they can be ignored in the calculation.

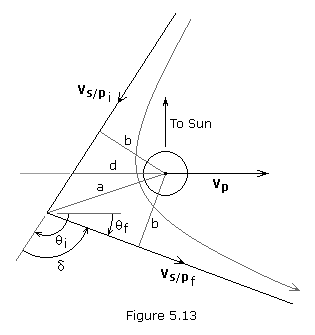
Figure 5.13 shows the motion of a spacecraft relative to a planet during a gravity assist maneuver. Encounters in space require the consideration of three dimensions; however, an approximate solution to the gravitational assist problem can be found using a simplified two-dimensional model. The following conditions are assumed:

• Orbits of planet and spacecraft are coplanar.
• Y-axis is parallel to the planet's position vector, positive outward from Sun.
• X-axis is in the orbital plane normal to the Y-axis, positive in the prograde direction.
• Planet's velocity (V_p) and flight path angle (_p) are given.
• Spacecraft's initial velocity (Vs_i), flight path angle (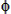s_i), and miss distance (d) are given.

The planet's velocity vector and the spacecraft's initial velocity vector are solved for using,

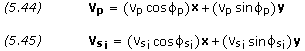
The initial relative velocity vector and its magnitude are solved for using,

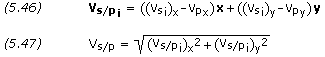
(Recall that V_∞ ≈ V_s/p)

The angle _i is obtained as follows (making sure to check quadrant),

The impact parameter, b, semi-major axis, a, and eccentricity, e, are solved for using equations (5.40), (5.41) and (5.42).

The turning angle, 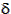, is solved for using equation (4.80), and the angle _f is calculated as follows,

The final relative velocity vector is,

And the spacecraft's final velocity vector and magnitude are,

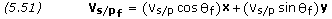
Finally, we calculate the spacecraft's final flight path angle as follows,

Click here for example problem #5.8

---

Compiled, edited and written in part by Robert A. Braeunig, 2012, 2013. 

Bibliography

http://www.braeunig.us/space/index.htm

Penulis : Drs.Simon Arnold Julian Jacob