ROCKET THERMODYNAMICS

R

ROCKET THERMODYNAMICS

---

• Enthalpy
• Adiabatic Flame Temperature
• Chemical Equilibrium
• Molecular Weight
• Specific Heat Ratio
• Condensed Species
• Isentropic Compression & Expansion
• STANJAN

---

A thorough understanding of thermodynamics is not a necessary requirement for the study of rocketry. As long as the temperature, molecular weight, of specific heat ratio of the exhaust products is known, the rocket equations can be solved. It is, however, often useful to be able to derive these quantities for one's self. In this article we provide an overview of the chemical thermodynamics applicable to rocket propulsion. It is assumed the reader has at least an elementary understanding of thermodynamics, as it is not our intent to fully explain the fundamentals.

Because of the complexity and tedious nature of the calculations, an easier method has been provided to readers of this web site. A series of propellant combustion charts are available from which one can obtain optimum mixture ratio, adiabatic flame temperature, gas molecular weight, and specific heat ratio for some common rocket propellants. These charts were developed using the methods described in this article.

Enthalpy

Enthalpy is a measure of the total energy of a thermodynamic system. It includes the internal energy, which is the energy required to create a system, and the amount of energy required to make room for it by displacing its environment and establishing its volume and pressure. The unit of measurement for enthalpy in the International System of Units (SI) is the joule, but other historical, conventional units are still in use, such as the BTU and the calorie.

The enthalpy is the preferred expression of system energy changes in many chemical, biological, and physical measurements, because it simplifies certain descriptions of energy transfer. This is because a change in enthalpy takes account of energy transferred to the environment through the expansion of the system under study.

The total enthalpy, H, of a system cannot be measured directly. Thus, change in enthalpy, ΔH, is a more useful quantity than its absolute value. The change ΔH is positive in endothermic reactions, and negative in heat-releasing exothermic processes. ΔH of a system is equal to the sum of non-mechanical work done on it and the heat supplied to it.

For quasistatic processes under constant pressure, ΔH is equal to the change in the internal energy of the system, plus the work that the system has done on its surroundings. This means that the change in enthalpy under such conditions is the heat absorbed (or released) by a chemical reaction. Enthalpies for chemical substances at constant pressure assume standard state: most commonly 1 bar (0.1 MPa) pressure. Standard state does not, strictly speaking, specify a temperature, but expressions for enthalpy generally reference the standard enthalpy of formation at 25^oC (298.15 K).

While H denotes the total enthalpy of a system, h is specific enthalpy, i.e. the enthalpy per mole or unit mass of a substance. We will simply refer to both as enthalpy, since the context will make it clear which is applicable.

The enthalpy of formation, or heat or formation, h^o_f , is the enthalpy of a substance at the base conditions of 25^oC and 0.1 MPa pressure. The enthalpy in any other state, relative to this base, would be found by adding the change of enthalpy between 25^oC and 0.1 MPa and the given state to the enthalpy of formation. That is, the enthalpy at any temperature and pressure, h_T,P, is

h_T,P = (h^o_f )_{298,0.1 MPa} + (Δh)_{298,0.1 MPa --> T,P}

where the term (Δh)_{298,0.1 MPa --> T,P} represents the difference in enthalpy between any given state and the enthalpy at 298.15 K, 0.1 MPa. For convenience we usually drop the subscripts in the examples that follow.

In most cases the substances that comprise the reactants and products in a chemical reaction are not at a temperature of 25^oC and a pressure of 0.1 MPa. Therefore the change of enthalpy between 25^oC and 0.1 MPa and the given state must be known. In the case of a solid or liquid, this change of enthalpy can usually be found from a table of thermodynamic properties or from specific heat data. In the case of gases, this change of enthalpy can be found as follows:

Assume ideal gas behavior between 25^oC, 0.1 MPa, and the given state. In this case, the enthalpy is a function of the temperature only, and can be found by use of an equation, from tabulated values of enthalpy as a function of temperature (which assumes ideal gas behavior), or calculated from specific heat capacity, C_p^o, where

NIST Chemistry WebBook provides equations for (h^o-h^o₂₉₈) and C_p^o for most substances, and tables can be generated using the web site NIST-JANAF Termochemical Tables. (h^o-h^o₂₉₈) is Δh, where h^o₂₉₈ refers to 25^oC or 298.15 K. The superscript ^o is used to designate that this is the enthalpy at 0.1 MPa pressure, based on ideal gas behavior, that is, the standard-state enthalpy.

When the deviation from ideal gas behavior is significant, other procedures must be employed, but that won't be necessary in our case.

Adiabatic Flame Temperature

Consider a given combustion process that takes place adiabatically and with no work or changes in kinetic or potential energy involved. For such a process the temperature of the products is referred to as the adiabatic flame temperature. With the assumptions of no work and no changes in kinetic or potential energy, this is the maximum temperature that can be achieved for the given reactants because any heat transfer from the reacting substances and any incomplete combustion would tend to lower the temperature of the products. For a given fuel and given pressure and temperature of the reactants, the maximum adiabatic temperature that can be achieved is with a stoichiometric mixture.

The following example shows how the adiabatic flame temperature may be found. The dissociation that takes place in the combustion products, which has a significant effect on the adiabatic flame temperature, will be considered in the next section.

Suppose we react a stoichiometric mixture of gaseous methane and gaseous oxygen at an initial temperature of 25^oC and 4 MPa pressure. Our reaction equation is

CH₄ + 2 O₂ CO₂ + 2 H₂O

We assume ideal gas behavior for all the constituents. In this case the first law of thermodynamics reduces to

H_R = H_P

_R n_i[h^o_f + Δh]_i = _P n_e[h^o_f + Δh]_e

where H_R is the enthalpy of the reactants, H_P the enthalpy of the products, h^o_f the enthalpy of formation of each constituent, Δh_i the change in enthalpy of each constituent in the reactants at the initial temperature, and Δh_e the change in enthalpy of each constituent in the products at the adiabatic flame temperature.

Below is a table giving enthalpy of formation and ideal gas enthalpy for several of the products that will result from a methane/oxygen reaction. Note that in the simplified reaction considered above, we have only CO₂ and H₂O on the right side of the equation. The additional substances will appear when we consider dissociation in the next section.

Temperature K	Methane CH4 (3/31/61)	Carbon Dioxide CO2 (9/30/65)	Carbon Monoxide CO (9/30/65)	Oxygen, Diatomic O2 (9/30/65)	Water (gas) H2O (3/31/61)	Hydrogen, Diatomic H2 (3/31/61)	Hydroxyl OH (3/31/66)
	(hfo)298 = -74.873 M = 16.043	(hfo)298 = -393.522 M = 44.010	(hfo)298 = -110.529 M = 28.010	(hfo)298 = 0 M = 31.999	(hfo)298 = -241.827 M = 18.015	(hfo)298 = 0 M = 2.0159	(hfo)298 = 39.463 M = 17.007
	(ho-ho298) kJ/mol	(ho-ho298) kJ/mol	(ho-ho298) kJ/mol	(ho-ho298) kJ/mol	(ho-ho298) kJ/mol	(ho-ho298) kJ/mol	(ho-ho298) kJ/mol
0	-10.024	-9.364	-8.669	-8.682	-9.904	-8.468	-9.171
100	-6.698	-6.456	-5.770	-5.778	-6.615	-5.293	-6.138
200	-3.368	-3.414	-2.858	-2.866	-3.280	-2.770	-2.975
298	0.000	0.000	0.000	0.000	0.000	0.000	0.000
300	0.066	0.067	0.054	0.054	0.063	0.054	0.054
400	3.861	4.008	2.975	3.029	3.452	2.958	3.033
500	8.200	8.314	5.929	6.088	6.920	5.883	5.991
600	13.130	12.916	8.941	9.247	10.498	8.812	8.941
700	18.635	17.761	12.021	12.502	14.184	11.749	11.903
800	24.675	22.815	15.175	15.841	17.991	14.703	14.878
900	31.205	28.041	18.397	19.246	21.924	17.682	17.887
1000	38.179	33.405	21.686	22.707	25.978	20.686	20.933
1100	45.549	38.894	25.033	26.217	30.167	23.723	24.025
1200	53.270	44.484	28.426	29.765	34.476	26.794	27.158
1300	61.302	50.158	31.865	33.351	38.903	29.907	30.342
1400	69.608	55.907	35.338	36.966	43.447	33.062	33.568
1500	78.153	61.714	38.848	40.610	48.095	36.267	36.840
1600	86.910	67.580	42.384	44.279	52.844	39.522	40.150
1700	95.853	73.492	45.940	47.970	57.685	42.815	43.501
1800	104.960	79.442	49.522	51.689	62.609	46.150	46.890
1900	114.212	85.429	53.124	55.434	67.613	49.522	50.308
2000	123.592	91.450	56.739	59.199	72.689	52.932	53.760
2100	133.087	97.500	60.375	62.986	77.831	56.379	57.241
2200	142.684	103.575	64.019	66.802	83.036	59.860	60.752
2300	152.371	109.671	67.676	70.634	88.295	63.371	64.283
2400	162.141	115.788	71.346	74.492	93.604	66.915	67.839
2500	171.984	121.926	75.023	78.375	98.964	70.492	71.417
2600	181.893	128.085	78.714	82.274	104.370	74.090	75.015
2700	191.862	134.256	82.408	86.199	109.813	77.718	78.634
2800	201.885	140.444	86.115	90.144	115.294	81.370	82.266
2900	211.958	146.645	89.826	94.111	120.813	85.044	85.918
3000	222.076	152.862	93.542	98.098	126.361	88.743	89.584
3200	242.431	165.331	100.998	106.127	137.553	96.199	96.960
3400	262.925	177.849	108.479	114.232	148.854	103.738	104.387
3600	283.536	190.405	115.976	122.399	160.247	111.361	111.859
3800	304.248	202.999	123.495	130.629	171.724	119.064	119.378
4000	325.045	215.635	131.026	138.913	183.280	126.846	126.934
4200	345.918	228.304	138.578	147.248	194.903	134.700	134.528
4400	366.855	241.003	146.147	155.628	206.585	142.624	142.156
4600	387.849	253.734	153.724	164.046	218.325	150.620	149.816
4800	408.893	266.500	161.322	172.502	230.120	158.682	157.502
5000	429.982	279.295	168.929	180.987	241.957	166.808	165.222
5200	451.110	292.123	176.548	189.502	253.839	174.996	172.967
5400	472.274	304.984	184.184	198.037	265.768	183.247	180.736
5600	493.469	317.884	191.832	206.593	277.738	191.556	188.531
5800	514.692	330.821	199.489	215.166	289.746	199.924	196.351
6000	535.942	343.791	207.162	223.756	301.796	208.346	204.192
The thermochemical data are calculated from the JANAF Thermochemical Tables, Thermal Research Laboratory, The Dow Chemical Company, Midland, Michigan. The date each table was issued is indicated.

Knowing the temperature of the reactants, we can easily calculate H_R. Since the reactant temperature in our example is equal to the base temperature of 25^oC, Δh_i = 0 and we need only to sum the enthalpies of formation of the reactants. From the table above we see that for diatomic oxygen (h_f^o)₂₉₈ = 0, which is typical for diatomic gases, and for methane we find (h_f^o)₂₉₈ = -74.873 kJ/mol. Therefore, we have

H_R = _i  n_i [h^o_f + Δh]_i = 1 × [-74.873 + 0] + 2 × [0 + 0] = -74.873 kJ

For the products, we have

H_P = _e  n_e [h^o_f + Δh]_e = 1 × [-393.522 + Δh_CO2] + 2 × [-241.827 + Δh_H2O] = -74.873 kJ

By trial-and-error solution, a temperature of the products is found that satisfies this equation. Suppose we've already performed several trials and have begun to hone in on a solution. For the next trial, assume T_P = 5,400 K.

H_P = 1 × [-393.522 + 304.984] + 2 × [-241.827 + 265.768] = -40.656 kJ

Since H_P > H_R, our assumed temperature is too high. Let's now try T_P = 5,200 K.

H_P = 1 × [-393.522 + 292.123] + 2 × [-241.827 + 253.839] = -77.375 kJ

We can now interpolate to find the adiabatic flame temperature.

T_P = (-74.873 – (-77.375)) / (-40.656 – (-77.375)) × (5,400 – 5,200) + 5,200 = 5,214 K

Cryogenic Reactants

From the preceding example it can be seen that the initial temperature of the reactants has an effect on the final temperature of the products. For storable propellants, temperature variations within the normal liquid range have only a small effect on engine performance. For hypergols, a 10^oC change in reactant temperature results in about 0.1% change in specific impulse. We can, therefore, safely assume that the initial temperature of storable propellants is the standard enthalpy of formation temperature of 25^oC. This assumption has the added benefit of simplifying the calculations as we need only look up the enthalpies of formations for the reactants without making any further adjustments for temperature.

Cryogenic propellants are another story, as their extremely low temperatures have a significant effect on performance. We must further take into consideration that the readily available thermochemical data for these substances is gaseous state rather than liquid. An adjustment must be made to account for the change of state.

Let's consider the example of cryogenic oxygen, which has a boiling point of -183^oC (90 K). We start with gaseous oxygen at 298 K, which has an enthalpy of formation of 0 kJ/mol. We then add the change in enthalpy required to lower the temperature from 298 K to 90 K. From the enthalpy tables we estimate that this adjustment is -6.06 kJ/mol. Next we deduct the enthalpy of vaporization to account for the change of state from gas to liquid. The enthalpy of vaporization of oxygen is 6.82 kJ/mol. Therefore, the enthalpy of liquid oxygen reactant is

h^o(liquid) = h^o_f + Δh_{298 -> 90} – Δh_vap = 0 – 6.06 – 6.82 = -12.88 kJ/mol

Chemical Equilibrium

We now turn our attention to chemical equilibrium. Here we will consider a chemical reaction involving only one phase, which is referred to as a homogeneous chemical reaction. In our case we will be considering a gaseous phase, but the basic considerations apply to any phase.

Consider a vessel that contains four compounds, A, B, C, and D, which are in chemical equilibrium at a given pressure and temperature. Let the number of moles of each component be designated n_A, n_B, n_C, and n_D. Further, let the chemical reaction that takes place between these four constituents be

v_AA + v_BB v_CC + v_DD

where the v's are the stoichiometric coefficients. It should be emphasized that there is a very definite relation between the v's (the stoichiometric coefficients) whereas the n's (the number of moles present) for any constituent can be varied simply by varying the amount of that component in the reaction vessel.

To determine the equilibrium composition for a chemical reaction, we must be able to determine the activity of the various constituents in the mixture. We do so by applying the concept of the equilibrium constant, K. Assuming the ideal gas model, which will be appropriate for our examples and applications, the chemical equilibrium equation can be written as

K = (y_C^V_C × y_D^V_D) / (y_A^V_A × y_B^V_B) × (P/P^o)^{V_C+V_D-V_A-V_B}

where y is the equilibrium mole fraction of the A, B, C and D constituents, v is the stoichiometric coefficient for each constituent, and the term P/P^o represents the ratio of pressure at which the reaction occurs to the standard state pressure.

The equation is written in this form because it demonstrates quite clearly the influence of various factors on the equilibrium composition (the y's). That is, we know that temperature and pressure both influence the equilibrium composition. It can be seen that the influence of temperature enters through the value of K (which is a function of temperature only) and the influence of pressure though the term (P/P^o)^{V_C+V_D-V_A-V_B}.

It should be noted that the equilibrium of combustion gases is very sensitive to temperature. Products existing at a high combustion temperature are very different from those existing at a lower combustion temperature. At high temperatures, dissociation of the products occurs, as the thermal energy causes the break up of molecules into simpler and monatomic constituents. Dissociation reactions are reversible (as indicated by the double arrow in the equations), so as the gases cool, recombination can occur.

Let's now revisit our previous example and employ a procedure for determing the equilibrium composition of the combustion products.

It is convenient to view the over-all process as though it occurred in two separate steps, a combustion process followed by a heating and dissociation of the combustion products. The combustion reaction is

CH₄ + 2 O₂ CO₂ + 2 H₂O

There are several dissociation reactions that will come into play, but we'll consider the two most dominant in this particular example.

CO₂ CO + 1/2 O₂

H₂O 1/2 H₂ + OH

That is, the energy released by the combustion of CH₄ and O₂ heats the CO₂ and H₂O to high temperature, resulting in the dissociation of part of the CO₂ to CO and O₂, and part of the H₂O to H₂ and OH. Thus, the overall reaction can be written

CH₄ + 2 O₂ a CO₂ + b CO + c O₂ + d H₂O + e H₂ + f OH

where the unknown coefficients a, b, c, d, e, and f must be found by solution of the equilibrium equations associated with the dissociation reactions.

From the combustion reaction we find that the initial compositions for the dissociation reactions are 1 mole CO₂ and 2 moles H₂O. Therefore, letting z' be the number of moles of CO₂ dissociated, and z" be the number of moles of H₂O dissociated, we find

                          CO2    CO   +   1/2 O2



     Initial:              1        0        0

     Change:               -z'      +z'      +z'/2

     _____________________________________________





     At equilibrium:     (1-z')     z'       z'/2

                          H2O    1/2 H2  +  OH



     Initial:              2        0         0

     Change:               -z"      +z"/2     +z"

     _____________________________________________
At equilibrium:     (2-z")     z"/2      z"

Therefore the overall reaction is

CH₄ + 2 O₂ (1-z') CO₂ + z' CO + z'/2 O₂ + (2-z") H₂O + z"/2 H₂ + z" OH

And the total number of moles at equilibrium for each reaction is

n' = (1-z') + z' + z'/2 = 1 + z'/2

n" = (2-z") + z"/2 + z" = 2 + z"/2

The equilibrium mole fractions are

y_CO2 = (1-z')/(1+z'/2)

y_CO = z'/(1+z'/2)

y_O2 = (z'/2)/(1+z'/2)

y_H2O = (2-z")/(2+z"/2)

y_H2 = (z"/2)/(2+z"/2)

y_OH = z"/(2+z"/2)

Substituting these quantities along with P = 4 MPa, we have the equilibrium equations.

K' = y_CO y_O2^1/2 / y_CO2 × (P/P^o)^1+1/2-1 = [z'/(1+z'/2)] × [(z'/2)/(1+z'/2)]^1/2 / [(1-z')/(1+z'/2)] × (4/0.1)^1/2

K" = y_H2 y_OH² / y_H2O² × (P/P^o)^1+2-2 = [(z"/2)/(2+z"/2)] × [z"/(2+z"/2)]² / [(2-z")/(2+z"/2)]² × (4/0.1)¹

Values of the equilibrium constants are found in the following table:

Logarithms to the Base e of the Equilibrium Constant K
Temperature K	CO2 = CO + 1/2 O2	H2O = 1/2 H2 + OH
298	-103.762	-106.208
500	-57.616	-60.281
1000	-23.529	-26.034
1200	-17.871	-20.283
1400	-13.842	-16.099
1600	-10.830	-13.066
1800	-8.497	-10.657
2000	-6.635	-8.728
2200	-5.120	-7.148
2400	-3.860	-5.832
2600	-2.801	-4.719
2800	-1.894	-3.763
3000	-1.111	-2.937
3200	-0.429	-2.212
3400	0.169	-1.576
3600	0.701	-1.009
3800	1.176	-0.501
4000	1.599	-0.044
4500	2.490	0.920
5000	3.197	1.689
5500	3.771	2.318
6000	4.245	2.843

By trial-and-error solution, a temperature of the products must be found that satisfies the equations. The steps are

• Select a trial value for T_P.
• Obtain ln(K) values from the table and calculate values of K.
• By trial-and-error, calculate the values of z.
• Calculate the number of moles of each product.
• Calculate the total enthalpy of the products.
• Compare the product enthalpy to the reactant enthalpy.
• If H_P ≠ H_R, select a new trial value of T_P and repeat.
• When close, interpolate to find final T_P.

Let's assume T_P = 3,600 K, we have

ln(K') = 0.701,   K' = 2.016,   z' = 0.4309

ln(K") = -1.009,   K" = 0.3646,   z" = 0.4587

CH₄ + 2 O₂ 0.5691 CO₂ + 0.4309 CO + 0.2154 O₂ + 1.5413 H₂O + 0.2294 H₂ + 0.4587 OH

H_P = -117.66 kJ/mol, which is < H_R

Assume T_P = 3,800 K and repeat.

ln(K') = 1.176,   K' = 3.241,   z' = 0.5285

ln(K") = -0.501,   K" = 0.6059,   z" = 0.5294

CH₄ + 2 O₂ 0.4715 CO₂ + 0.5285 CO + 0.2643 O₂ + 1.4706 H₂O + 0.2647 H₂ + 0.5294 OH

H_P = -35.94 kJ/mol, which is > H_R

Calculate adiabatic flame temperature by interpolation.

T_P = (-74.873 – (-117.66)) / (-35.94 – (-117.66)) × (3,800 – 3,600) + 3,600 = 3,705 K

Knowing the temperature, we can now interpolate to find the corresponding values of ln(K) and calculate the equilibrium mixture.

ln(K') = 0.950,   K' = 2.586,   z' = 0.4949

ln(K") = -0.742,   K" = 0.4762,   z" = 0.4814

CH₄ + 2 O₂ 0.5186 CO₂ + 0.4814 CO + 0.2407 O₂ + 1.5051 H₂O + 0.2474 H₂ + 0.4949 OH

For a more accurate solution, there are additional dissociation reactions that have to be considered, such as

H₂O H₂ + 1/2 O₂

H₂ 2 H

O₂ 2 O

It is evident from this rather simple example that accounting for all the possible dissociations requires the solving of a great many simultaneous equations. Consider adding another element to the mixture, such as nitrogen, and we've complicated the problem even further. Providing accurate solutions quickly and easily can only be performed with the aid of a computer program. One such program is the freeware STANJAN, written by former Stanford University Professor William C. Reynolds, © 1984.

Below is the STANJAN solution to the same methane/oxygen example that we've been examining. Note that after all the dissociations have been accounted for, the final adiabatic flame temperature has been lowered to 3,553.87 K.

Independent relative element system atom population potential C 1.00000000E+00 -16.8393 O 4.00000000E+00 -14.9514 H 4.00000000E+00 -10.3070 Composition at T = 3553.87 K P = 3.948E+01 atmospheres species mol fraction mass fraction mol fraction in the gas in mixture in mixture gas phase CO .14455E+00 .17980E+00 .14455E+00 CO2 .13679E+00 .26734E+00 .13679E+00 H .25470E-01 .11400E-02 .25470E-01 HO .93941E-01 .70948E-01 .93941E-01 H2 .58263E-01 .52158E-02 .58263E-01 H2O .44472E+00 .35579E+00 .44472E+00 O .23960E-01 .17023E-01 .23960E-01 O2 .72308E-01 .10275E+00 .72308E-01 Mixture properties: gas molal mass = 22.519 kg/kmol T = 3553.866 K P = 4.0000E+06 Pa V = 3.2803E-01 m**3/kg U =-2.2476E+06 J/kg H =-9.3544E+05 J/kg S = 1.1981E+04 J/kg-K Made 3 (T,P) iterations; 0 condensate iterations; 31 gas passes.

Molecular Weight

The average molecular weight, M, of a mixture is simply

M = m / n

where n is the total number of moles in the mixture, and m is the total mass of the mixture. The total moles and total mass are found by

n = _i n_i

m = _i (n_i × M_i)

where n_i is the number of moles of each constituent, M_i is the molecular weight of each constituent.

Referring back to the last iteration of our combustion equation, we have

CH₄ + 2 O₂ 0.5186 CO₂ + 0.4814 CO + 0.2407 O₂ + 1.5051 H₂O + 0.2474 H₂ + 0.4949 OH

Calculating the molecular weight of the mixture, we have

n = 3.4881 moles,   m = 80.040 g

M = 80.040 / 3.4881 = 22.947 g/mol

Alternatively, if the mole fraction, y_i, of each constituent is given, where y_i = n_i / n, the average molecular weight is found by

M = _i (y_i × M_i)

Referring to the STANJAN run above, we can see that both the mole fraction and the gas molecular weight is given, where M = 22.519 kg/kmol. This is lower than our derived unit because our example failed to take into consideration all the applicable dissociations.

Specific Heat Ratio

The constant-pressure specific heat, or heat capacity, C_p, and the constant-volume specific heat, C_v, are useful functions for thermodynamic calculations, particularly for gases, and are defined by the following relationships

C_p = (∂h/∂T)_p

C_v = (∂u/∂T)_v

where h is specific enthalpy, u is specific internal energy, and T is temperature.

A very important relationship between the constant-pressure and constant-volume specific heats of an ideal gas is found in the equation

C_p – C_v = R'

where C_p and C_v are on a mole basis, and R' is the universal gas constant (8.31446 J/mol-K). This tells us that the difference between the constant-pressure and constant-volume specific heats of an ideal gas is always constant, though both are a function of temperature.

Many thermodynamic solutions use the ratio of the specific heats, k or 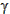, defined as

k = C_p / C_v

Since it is common for thermodynamic references to provide the value of C_p only, from which C_v is calculated, we can combine equations and write

k = 1 / (1 - R' / C_p)

Values of constant-pressure specific heat are typically found by use of an equation, or from tabulated values of C_p as a function of temperature. The Shomate equation is commonly used, which is shown below along with the Shomate coefficients of the products found in our combustion example.

Gas Phase Heat Capacity (Shomate Equation)
Cpo = A + Bt + Ct2 + Dt3 + E/t2 where Cp = heat capacity (J/mol-K), t = Temperature (K) / 1000
Formula	Temp. Range	A	B	C	D	E
CO2	1200-6000	58.16639	2.720074	-0.492289	0.038844	-6.447293
CO	1300-6000	35.15070	1.300095	-0.205921	0.013550	-3.282780
H2O	1700-6000	41.96426	8.62253	-1.499780	0.098119	-11.15764
H2	2500-6000	43.413560	-4.293079	1.272428	-0.096876	-20.533862
H	298-6000	20.78603	4.850638x10-10	-1.582916x10-10	1.525102x10-11	3.196347x10-11
O2	2000-6000	20.91111	10.72071	-2.020498	0.146449	9.245722
O	2500-6000	22.18977	-1.318044	0.378308	-0.026069	0
OH	1300-6000	28.74701	4.714489	-0.814725	0.054748	-2.747829
Shomate coefficients obtained from NIST Chemistry WebBook, except monatomic oxygen (O) derived by R.A. Braeunig from data found here.

Calculating the specific heat ratio of a single substance is straightforward. Say we have carbon monoxide at 3,000 K, the specific heat ratio is

From Shomate equation, C_p = 36.8736 J/mol-K

k = 1 / (1 - 8.31446 / 36.8736) = 1.2911

When we have a mixture of gases, we must determine the specific heat of the mixture, where

C_pgas = 1 / n × _i (n_i × Cp_i)   , or

C_pgas = _i (y_i × Cp_i)

Let's calculate the specific heat ratio for the mixture of gases found in the STANJAN solution to our methane/oxygen problem, noting that the temperature is 3,553.87 K.

C_pgas = _i (y_i × Cp_i) = 49.0786 J/mol-K

k = 1 / (1 - 8.31446 / 49.0786) = 1.2040

Although some computer programs calculate the value of specific heat ratio, STANJAN does not. If STANJAN is used, the user will have to calculate k separately, though this can easily be done through the use of spreadsheet software.

Condensed Species

Everything so far has assumed the combustion products consist of a homogenous mixture of gases. When dealing with liquid rocket propellants, this is a fair assumption, as any condensed species (either liquids or solids) will appear in trace quantities only. However, when dealing with solid propellants, a significant portion of the exhaust products will be in a condensed phase, which is evident as visible smoke in the exhaust plume. When the products exist in more than one phase, the mixture is said to be heterogeneous.

Heterogeneity requires that we alter the method by which we calculate the molecular weight and specific heat ratio. The two-phase equations presented below are those derived by Richard Nakka and described in his Experimental Rocketry Web Site.

A key assumption required is that the condensed-phase particles flow at the same velocity as the gas (i.e. no velocity lag), so the modified equations represent an upper limit on performance. The details are too involved to present here, so only the final outcome is presented, which fortunately, is quite simple. As it turns out, the gas-particle mixture behaves like a gas with a modified specific heat ratio, k. All the fundamental equations remain the same and are fully applicable to two-phase flow, with the only modifications being as follows:

• Molecular weight, M, must take into account the presence of the condensed-phase by calculating the effective molecular weight, which is found by dividing the total system mass, m, by the number of moles of gas in the system, n.
  
  
  M _(effective) = m _(total) / n _(gas)
  
  
• The modified specific heat ratio, also called isentropic exponent, takes two forms, one for conditions where flow velocity (or actually, acceleration) is low, and the other for conditions of flow with high acceleration. Where flow acceleration is low, such as in the combustion chamber,
  
  
  k_mix = 1 / (1 - R' / C_pmix)
  
  
  where C_pmix is the effective specific heat of the gas and condensed-phase mixture, given by
  
  
  C_pmix = 1 / n × [ 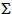_i (n_i × Cp_i) + n_s × C_s]
  
  
  where n_i is the number of moles of gas component i, n_s the number of moles of condensed-phase component, and n the total number of gas moles.
  k_mix is the form to use when calculating combustion chamber pressure and characteristic exhaust velocity.
  Where flow velocity and acceleration are high, that is, in the nozzle, we have
  
  
  k_2ph = k' × [(1 + Ψ × C_s / C_pgas) / (1 + k' × Ψ × C_s / C_pgas)]
  
  
  where k' is the specific heat ratio for the gas only mixture; Ψ = w_s /(1–w_s), where w_s is the mass fraction of condensed-phase particles in the exhaust; C_s is the specific heat for the solid (or liquid) mixture in the exhaust; and C_pgas is the specific heat for the gas only mixture. As before,
  
  
  C_pgas = 1 / n_gas × 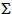_i (n_i × Cp_i)
  
  
  
  k' = 1 / (1 - R' / C_pgas)
  
  
  The derivation of this form of modified specific heat ratio assumes a frozen flow condition where no thermal or velocity particle lag is assumed to exist, and is based on the momentum and energy equations for steady isentropic flow.
  k_2ph is the form to use when calculating exhaust velocity, thrust, thrust coefficient and the other nozzle flow parameters.

Let's now consider an example. Below is a STANJAN run for the combustion of 68% ammonium perchlorate, 18% aluminum, and 14% HTPB at a chamber pressure of 4 MPa.

Independent relative element system atom population potential Al 6.67111407E-01 -16.5165 Cl 5.78772661E-01 -20.5197 O 2.31509064E+00 -19.0205 H 3.86805792E+00 -9.2472 C 1.03531152E+00 -12.1297 N 5.78772661E-01 -13.7827 Composition at T = 3280.36 K P = 3.948E+01 atmospheres species mol fraction mass fraction mol fraction in the gas in mixture in mixture gas phase Al .15875E-03 .15634E-03 .14634E-03 AlCl .82935E-02 .18897E-01 .76450E-02 AlClO .13303E-02 .38081E-02 .12263E-02 AlCl2 .22637E-02 .80879E-02 .20867E-02 AlCl3 .21732E-03 .10576E-02 .20033E-03 AlO .14196E-03 .22269E-03 .13086E-03 AlOH .42786E-03 .68696E-03 .39441E-03 AlO(OH) .29780E-03 .65205E-03 .27452E-03 CO .27553E+00 .28168E+00 .25398E+00 CO2 .81351E-02 .13067E-01 .74990E-02 Cl .82798E-02 .10713E-01 .76324E-02 H .33101E-01 .12178E-02 .30513E-01 HCl .13549E+00 .18031E+00 .12490E+00 HO .30828E-02 .19136E-02 .28418E-02 H2 .36159E+00 .26606E-01 .33332E+00 H2O .82105E-01 .53989E-01 .75685E-01 NO .18270E-03 .20010E-03 .16842E-03 N2 .79197E-01 .80974E-01 .73005E-01 O .16856E-03 .98432E-04 .15538E-03 condensed species Al2O3(c) .31566E+00 .78192E-01 Mixture properties: gas molal mass = 18.750 kg/kmol T = 3280.363 K P = 4.0000E+06 Pa V = 2.4894E-01 m**3/kg U =-2.8456E+06 J/kg H =-1.8499E+06 J/kg S = 9.6821E+03 J/kg-K Made 3 (T,P) iterations; 11 condensate iterations; 54 gas passes.

To perform the calculations, we require the molecular weight and specific heat of each constituent. The following is obtained from the NIST Chemistry WebBook, with C_p valves derived for the chamber temperature of 3280.363 K.

     Species          M           Cp

                    g/mol      J/mol-K    

     ---------------------------------

     AlCl          62.435      39.0550

     Al            26.982      20.7692
AlClO         78.434      62.2791

     AlO           42.981      46.9917
AlCl2         97.888      58.3019
     AlCl3        133.341      83.0688
     AlOH          43.989      60.2511

     Cl            35.453      20.9928
AlO(OH)       59.988      81.6723
     CO            28.010      37.3728
     CO2           44.010      62.5638
     H              1.008      20.7860

     NO            30.006      37.6115
HCl           36.461      37.5480
     HO            17.007      37.1224
     H2             2.016      37.6952
     H2O           18.015      56.5356
     N2            28.013      37.2055


O             15.999      21.0168

     Al2O3(c)     101.961     192.4640

Referring to the "mol fraction in mixture" in the STANJAN run, we find

n_s = 0.078192 mole

n = 1 – 0.078192 = 0.921808 mole (also attainable by summing the gas constituents)

And from "mass fraction in mixture", we find the mass fraction of the condensed species,

w_s = 0.31566

Calculating the total mass, we have

m = _i (n_i × M_i) = 25.256 g/mol

Therefore,

M = 25.256 / 0.921808 = 27.398 g/mol

Further, we find

_i (n_i × Cp_i) = 35.6887 J/mol-K

C_s = 192.4640 J/mol-K

C_pgas = 1 / 0.921808 × 35.6887 = 38.7160 J/mol-K

C_pmix = 1 / 0.921808 × (35.6887 + 0.078192 × 192.4640) = 55.0417 J/mol-K

Finally, we calculate the specific heat ratios,

k_mix = 1 / (1 – 8.31446 / 55.0417) = 1.1779

k' = 1 / (1 – 8.31446 / 38.7160) = 1.2735

Ψ = 0.31566 / (1 - 0.31566) = 0.46126

k_2ph = 1.2735 × [(1 + 0.46126 × 192.4640 / 38.7160) / (1 + 1.2735 × 0.46126 × 192.4640 / 38.7160)] = 1.0698

When to use k_mix versus k_2ph

Referring to the Rocket Propulsion page, when condensed species are present, the following equations should be solved using k_mix:

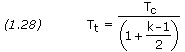
And the following should be solved using k_2ph:

Isentropic Compression & Expansion

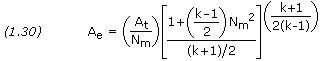
Here we present two important equations that relate the pressure, temperature, and volume that a gas occupies during reversible compression or expansion. Such a process occurs during the compression and power strokes for an internal combustion engine. The same equations describe the conditions across the compressor and turbine of a gas turbine, or across the nozzle of a rocket engine. The resulting compression and expansion are reversible processes in which the entropy of the system remains constant. Such a process is called an isentropic process.

For isentropic compression and expansion, the effect of pressure on temperature is described by

T₂ / T₁ = (p₂ / p₁)^{1 – 1 / k}

and the effect of volume on pressure is

p₂ / p₁ = (v₁ / v₂)^k

where T₁, p₁ and v₁ are the initial temperature, pressure and volume; T₂, p₂ and v₂ are the final temperature, pressure and volume; and k is the specific heat ratio.

We can also combine equations to find the effect of volume on temperature

T₂ / T₁ = (v₁ / v₂)^{k – 1}

Since the expansion of exhaust gases through a rocket nozzle is an isentropic process, the above equations are applicable. Say, for instance, we want to know the temperature at the nozzle exit for a rocket engine having a chamber temperature of 3,250 K, a chamber pressure of 6 MPa, a nozzle exit pressure of 0.07 MPa, and k is known to be 1.23. We have

T₂ / 3250 = (0.07 / 6)^{1 – 1 / 1.23}

T₂ = 1,414 K

STANJAN

Should you decide to give STANJAN a try, I have some helpful tips learned through my experience using it. This is not instructions on how to use the software.

First, STANJAN comes with a file named TURBINE.DOC that is an example of a STANJAN run for a gas turbine problem. It outlines the steps for finding adiabatic flame temperature and for finding the results of isentropic expansion of the exhaust. Learn to follow this example and you should be able to perform all the calculations described in this article.

Second, STANJAN comes with a limited number of species data files, so you're certainly going to have to create some of your own if you plan to get serious about using the software. Included with STANJAN is a file named SPECIES.DOC that explains how the data files are formatted. Below is an excerpt showing a sample data entry for carbon dioxide.

Species name (8 chars) Atomic composition: Left justified in Col 1 | number right justified in | Date of data the field followed by | 8 chars starting Col 10 atom symbols (2 chars) | | left justified in the | | Cols 19-28 field (upper or lower | | mol. wt, g/mol case, but you must use | | | the same characters for a | | | cols 29-38 given atom throughout | | | enth. form the data file). Must be | | | at 298.15K, positioned as below; | | | kcal/mol 6(I3,A2) starting in | | | | col 49. | | | | Cols 39-48 . | | | | 0.0 for gas; . | | | | density, g/cc . | | | | for liquid or . | | | | solid ............................... | | | | | | | | | | | | | | | | | .. | .. | .. | .. | .. | .. CO2 9/30/65 44.00995 -94.054 0.000 1C 2O 0 0 0 0 47.769 51.072 51.127 53.830 56.122 58.126 59.910 61.522 62.992 64.344 65.594 66.756 67.841 68.859 69.817 70.722 71.578 72.391 73.165 73.903 74.608 75.284 75.931 76.554 77.153 77.730 78.286 78.824 79.344 79.848 80.336 80.810 81.270 81.717 82.151 82.574 82.986 83.388 83.780 84.162 84.536 84.901 85.258 85.607 85.949 86.284 86.611 86.933 87.248 87.557 87.860 88.158 88.451 88.738 89.021 89.299 89.572 89.841 90.106 90.367 -0.816 0.000 0.016 0.958 1.987 3.087 4.245 5.453 6.702 7.984 9.296 10.632 11.988 13.362 14.750 16.152 17.565 18.987 20.418 21.857 23.303 24.755 26.212 27.674 29.141 30.613 32.088 33.567 35.049 36.535 38.024 39.515 41.010 42.507 44.006 45.508 47.012 48.518 50.027 51.538 53.051 54.566 56.082 57.601 59.122 60.644 62.169 63.695 65.223 66.753 68.285 69.819 71.355 72.893 74.433 75.976 77.521 79.068 80.617 82.168 Lines 2-7 are the values of S(T,1 atm), cal/mol-K, as read from the JANNAF tables at 200, 298.15,300,400,500,....,6000 K. Lines 8-13 are the values of H-H(298.15), kcal/mol, as read from the JANNAF tables at 200, 298.15,300,400,500,....,6000 K.

STANJAN already includes the gaseous species you'll commonly encounter in most combustion reactions, that is, those containing C, H, N and O. This will suffice for calculations involving most liquid propellants. However, if you plan to perform calculations involving solid propellants, new elements will be introduced into the exhaust, such as Al and Cl. This will necessitate the creation of an entirely new group of species data files.

Data files can be easily edited and/or created in a text editor such as Notepad or WordPad. The values that populate the data files can be found and/or calculated using NIST Chemistry WebBook or, even easier, using NIST-JANAF Thermochemical Tables. Be advised, however, that the STANJAN data files use units of calories instead of Joules. The NIST Chemistry WebBook allows the selection of either calorie-based or Joule-based data. The NIST-JANAF Thermochemical Tables site, although presenting the data in a more convenient format, must be converted from Joules to calories, where 1 calorie = 4.184 Joules.

You will most definitely need to create you own data files for the reactants, as STANJAN doesn't include any of the common rocket propellants. However, there's a short cut that greatly simplifies this task. If you always assume that your reactants are at an initial temperature of 298.15 K, i.e. the base temperature, there is no need to populate the data files with all the S and H-H(298.15) data, as this is used only when the temperature varies from 298.15 K. You need to complete the data on the first line only, making your reactant data files look like the following example for methyl hydrazine:

CH6N2 1951 46.07170 12.940 0.866 1C 6H 2N 0 0 0 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000

Of course, assuming a temperature of 298.15 K appears, at first, to be a problem when using cryogenic propellants, but there's a way around this. Besides, STANJAN allows a minimum starting temperature of 200 K, so we can't set our reactants to cryogenic temperatures even if we wanted to. Furthermore, STANJAN doesn't allow reactants of different temperatures, so it can't handle a scenario like RP-1 and LOX, where the temperatures are vastly different.

The solution is a simple trick; in the field where you would normally enter the enthalpy of formation, replace this with the enthalpy of the cryogenic liquid at its boiling point. I earlier demonstrated this when calculating the enthalpy of LOX to be -12.88 kJ/mol, or -3.078 kcal/mol. Now when entering a temperature of 298.15 K, you'll actually get the enthalpy of the cryogenic liquid.

Finally, I like to create separate data files for the reactants and the products. And for the products I like to create several data files, each one representing a different group of elements. For example, I have data files HO.DAT, CHO.DAT, CHNO.DAT, etc. Thus, if my reaction contains only the elements C, H and O, I'll select the file CHO.DAT, which contains all the constituents normal to such a reaction – C, CO, CO₂, H, H₂, HO, H₂O, O and O₂. This reduces the number of keystrokes require versus having to select the applicable constituents from an all-inclusive list of products.

STANJAN will operate on a PC running Windows XP or earlier. It will also work with Windows 7 Professional in XP Mode. Whether or not it will run on other platforms is unknown.

---

Compiled, edited and written in part by Robert A. Braeunig, 2012. 

Bibliography

http://www.braeunig.us/space/index.htm

Penulis : Drs.Simon Arnold Julian Jacob